辉县市作为河南省的一个县级市,其招聘信息主要来源于几个官方和主流渠道,由于招聘信息具有时效性,最准确的方式是直接访问官方平台,以下我将为您分类整理,并提供查询方法。

主要招聘信息来源渠道
这是查找辉县市招聘信息最权威、最可靠的途径,建议您优先关注:
-
辉县市人民政府官方网站
- 网址:
www.huixian.gov.cn - 查找路径: 访问网站后,通常在首页的“信息公开”、“公示公告”或“人事信息”等栏目中查找,这是发布政府机关、事业单位招聘信息的首选平台。
- 网址:
-
辉县市人力资源和社会保障局官网/公众号
- 这是发布事业单位、国有企业、部分政府购买服务岗位招聘的核心平台。
- 官网: 通常在市政府官网的“部门链接”中可以找到“人力资源和社会保障局”,进入后查找“通知公告”、“事业单位招聘”等栏目。
- 微信公众号: 搜索“辉县人社”或类似的官方公众号,这是获取最新、最快招聘通知的绝佳方式,通常会第一时间发布招聘简章、报名入口和考试通知。
-
辉县市融媒体中心 / 辉县发布

- 微信公众号: 搜索“辉县发布”。
- 作用: 作为市委市政府的官方信息发布平台,会转发一些重要的、社会关注度高的招聘信息,特别是教育、医疗等系统的大规模招聘。
-
主流招聘网站
- 前程无忧、智联招聘、BOSS直聘、猎聘等。
- 查找方法: 在这些网站的搜索栏中,选择地点为“新乡市”或“辉县市”,关键词可以设置为“事业单位”、“教师”、“医生”、“国企”等,这里不仅有政府发布的招聘,还有很多本地企业、民办学校的招聘信息。
按招聘单位类型分类
辉市市的招聘主要可以分为以下几类,您可以根据自己的情况重点关注:
事业单位招聘
这是每年招聘的“重头戏”,通常由辉县市人社局统一组织。
- 招聘单位: 各乡镇政府、市直机关下属的事业单位(如:教育局、卫健委、财政局、文旅局等下属的二级机构)。
- 招聘岗位:
- 教师类: 幼儿园、小学、中学各学科教师,这是招聘人数最多的类别之一。
- 医疗类: 各乡镇卫生院、市属医院的专业技术人员(医生、护士、医技人员等)。
- 综合类: 会计、文秘、计算机、工程技术等管理或专业技术岗位。
- 特点: 通常有编制(部分岗位为备案制或合同制),考试科目为《公共基础知识》和《职业能力测验》等,竞争比较激烈。
- 关注时间: 全年都有,但高峰期通常在上半年(3-6月)和下半年(9-11月)。
政府购买服务/劳务派遣岗位
这类岗位数量也很多,虽然没有事业编制,但工作稳定,是进入体制内工作的一个重要途径。
- 招聘单位: 通常是各乡镇、市直机关单位。
- 招聘岗位: 执法辅助、文员、后勤服务、网格员、社区工作者等。
- 特点: 由第三方劳务派遣公司签订合同,工资待遇由财政统一拨付,工作内容和性质与在编人员相似。
- 关注时间: 招聘比较灵活,常年都有,需要密切关注“辉县人社”公众号和各乡镇的公告。
国有企业招聘
- 招聘单位: 辉县市属或驻辉的国有企业,
- 辉县市投资集团有限公司及其下属子公司。
- 河南孟电集团等本地知名企业。
- 供电、供水、燃气等公共服务类国企。
- 招聘岗位: 财务、工程、行政、技术员、营销等。
- 特点: 待遇较好,相对稳定,招聘信息通常发布在国企官网或“辉县人社”公众号。
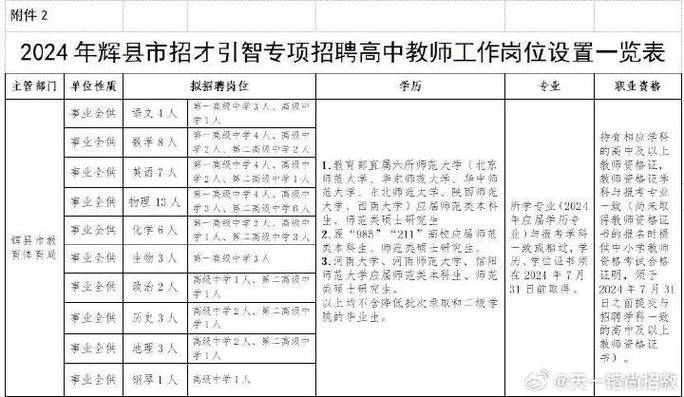
教育系统专项招聘
除了事业单位统招中的教师岗,有时教育局会单独组织教师招聘,特别是为了解决教师短缺问题。
- 关注重点: “辉县发布”、“辉县人社”以及辉市教育局的官方信息。
医疗系统专项招聘
与教育系统类似,卫健委或市医院有时也会单独组织招聘。
- 关注重点: “辉县人社”以及辉县市卫生健康委员会、辉县市人民医院等医疗机构的官方信息。
近期招聘信息示例(请以官方发布为准)
由于招聘信息实时变动,以下仅为示例,帮助您了解招聘的大致形式和内容。请务必忽略具体时间,以最新官方公告为准。
【示例一:202X年辉县市事业单位公开招聘工作人员公告】
- 招聘岗位: 招聘教师150名,医护人员80名,综合类岗位50名。
- 报名条件:
- 具有中华人民共和国国籍。
- 遵守宪法和法律。
- 年龄一般在18周岁以上、35周岁以下(部分岗位可放宽)。
- 具有岗位所需的学历、专业和资格条件(如教师资格证、执业医师证等)。
- 报名时间: 202X年X月X日9:00至X月X日17:00。
- 报名方式: 通过辉县市人力资源和社会保障局官网进行网上报名。
- 笔试科目为《职业能力测验》和《公共基础知识》。
【示例二:辉XX镇公开招聘网格员公告】
- 招聘岗位: 若干名。
- 报名条件: 辉县市户籍,大专及以上学历,年龄在40周岁以下,熟悉电脑操作。
- 薪资待遇: 每月XXXX元,缴纳五险。
- 报名方式: 到辉XX镇党政办公室现场报名。
报名及备考建议
- 及时关注: 将“辉县人社”和“辉县发布”的微信公众号设为星标,每天查看,不错过任何重要通知。
- 准备材料: 提前准备好身份证、毕业证、学位证、学历认证报告、相关资格证书(如教师资格证、执业医师证等)的扫描件和电子版。
- 明确方向: 根据自己的专业、学历和兴趣,确定要报考的岗位类型,提前了解该类岗位的考试大纲和历年真题。
- 诚信报考: 仔细阅读招聘公告,确保自己符合所有报考条件,诚信填写报名信息。
想获取最准确、最及时的辉县市招聘信息,最佳途径是“辉县人社”的官方微信公众号和辉县市人民政府官网,请务必以这两个官方渠道发布的信息为准,警惕非官方渠道的虚假招聘信息。
祝您求职顺利!