这是一个非常严重且违法的问题,外包公司不为员工缴纳“五险一金”(社会保险和住房公积金)是明确违反中国法律法规的行为,这不仅损害了员工的切身利益,也扰乱了正常的用工市场秩序。

下面我将为您详细解析这个问题,包括其违法性、对员工的危害、员工可以采取的维权途径以及一些特殊情况。
为什么外包公司不缴五险一金是违法的?
根据中国《中华人民共和国劳动合同法》、《中华人民共和国社会保险法》和《住房公积金管理条例》的规定:
- 劳动关系是缴纳的前提:只要员工与用人单位之间存在事实劳动关系(即接受单位管理、从事单位安排的工作、单位支付劳动报酬),单位就有法定义务为员工缴纳五险一金。
- 外包不等于免责:外包是一种业务合作模式,但不能免除用人单位的法律责任,员工与外包公司签订劳动合同,或虽然没有合同但存在事实劳动关系,外包公司就是法定的用人单位,必须承担缴纳五险一金的义务,不能以“用工单位(甲方)没给钱”或“员工是劳务派遣/外包”为借口。
- 法律明确规定:
- 《社会保险法》第五十八条:用人单位应当自用工之日起三十日内为其职工向社会保险经办机构申请办理社会保险登记。
- 《住房公积金管理条例》第十五条:单位录用职工的,应当自录用之日起30日内向住房公积金管理中心办理缴存登记。
无论是什么用工形式(正式员工、劳务派遣、业务外包),只要存在劳动关系,缴纳五险一金就是用人单位的强制性、法定性义务,没有任何商量余地。
不缴纳五险一金对员工的巨大危害
这是最核心的问题,直接关系到员工的未来和保障。

社会保险(五险)的危害:
-
养老保险:
- 影响退休金:缴费年限和缴费基数直接决定退休后能领取多少养老金,不缴或少缴,意味着未来退休后的生活质量会严重下降。
- 无法享受终身医疗:养老保险累计缴费满15年是领取养老金的基本条件,也是享受终身医保待遇的前提之一。
-
医疗保险:
- 看病无法报销:没有医保,员工看病、买药、住院等所有医疗费用都需要自己全额承担,经济压力巨大。
- 无法享受医保卡个人账户:医保卡里的个人账户余额可用于支付日常购药等费用,不缴则没有。
-
失业保险:
- 失业后无收入来源:非因本人意愿中断就业的,符合条件可以领取失业保险金,保障基本生活,不缴则无法享受这项保障。
-
工伤保险:

- 工伤无人买单:这是最危险的!工作中一旦发生意外伤害或患职业病,所有医疗费用、伤残补助金、工亡赔偿等都将由员工自己承担,工伤保险是员工的生命保障线。
-
生育保险:
- 无法享受生育待遇:女员工生育期间的生育津贴、产假工资、产前检查和分娩费用报销等都无法享受,男员工也没有相应的陪产假待遇。
住房公积金的危害:
- 无法贷款买房:没有连续缴存公积金,就无法申请公积金贷款,公积金贷款的利率远低于商业贷款,能节省几十万的利息。
- 无法提取租房:在大城市,符合条件的员工可以提取公积金支付房租,不缴则失去了这项福利。
- 无法应对大额开支:公积金还可以用于房屋装修、大病治疗等,是一项重要的储蓄和保障。
员工可以采取的维权途径
如果遇到外包公司不缴纳五险一金的情况,员工可以采取以下步骤维权:
第一步:沟通与协商
尝试与公司的人力资源部门或管理层进行沟通,明确指出其行为的违法性,要求其依法补缴,公司可能是出于疏忽或侥幸心理,沟通后可能会改正。
第二步:收集和保存证据
这是维权成功的关键,需要收集能够证明劳动关系的证据,
- 劳动合同(最重要的证据)
- 工资条、银行流水(显示公司名称的工资发放记录)
- 工牌、工作证、入职登记表
- 盖有公司公章的文件、工作邮件、聊天记录
- 考勤记录(打卡截图、加班记录等)
- 同事的证言
第三步:向劳动监察部门投诉
这是最直接、最有效的官方途径。
- 投诉部门:当地人力资源和社会保障局下的劳动保障监察大队。
- 方式:
- 电话投诉:拨打全国统一劳动保障咨询投诉电话 12333。
- 现场投诉:前往公司注册地或经营所在地的劳动监察大队进行投诉。
- 线上投诉:通过当地人社局官网、微信公众号等渠道进行举报。
- 处理:劳动监察大队接到投诉后,会进行调查核实,如果情况属实,他们会向公司下达《劳动保障监察限期改正指令书》,责令公司在规定期限内为员工补缴五险一金,如果公司拒不执行,监察部门可以申请法院强制执行。
第四步:申请劳动仲裁
如果除了五险一金,还有其他劳动争议(如拖欠工资),或者对投诉处理结果不满意,可以申请劳动仲裁。
- 机构:公司注册地或劳动合同履行地的劳动人事争议仲裁委员会。
- 时效:劳动仲裁的时效一般为一年,从当事人知道或应当知道其权利被侵害之日起计算,对于补缴社保,部分地区支持追溯2-3年。
- 注意:劳动仲裁是诉讼的前置程序,必须先经过仲裁才能向法院起诉。
第五步:提起诉讼
如果对仲裁结果不服,可以在收到仲裁裁决书之日起15日内向人民法院提起诉讼。
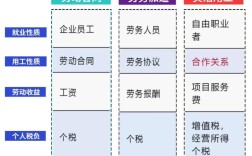
特殊情况:劳务派遣 vs. 业务外包
很多人会混淆这两个概念,它们在五险一金缴纳上的责任方是不同的。
-
劳务派遣:
- 关系:员工与劳务派遣公司签订劳动合同,但实际在用工单位工作。
- 责任:劳务派遣公司是法定的用人单位,必须为员工缴纳五险一金,用工单位只是实际使用员工,承担同工同酬等责任。
-
业务外包:
- 关系:发包方(用工单位)将某个业务整体外包给外包公司,由外包公司自行组织人员完成。
- 责任:员工与外包公司建立劳动关系,因此外包公司是缴纳五险一金的法定义务人,发包方不直接承担此责任,但如果外包公司是“假外包、真派遣”,用工单位可能需要承担连带责任。
如何区分? 关键看管理关系,如果用工单位直接对员工进行考勤、分配任务、绩效考核,那么很可能就是“假外包、真派遣”,员工可以主张与用工单位存在事实劳动关系。
总结与建议
- 明确法律底线:外包公司不缴五险一金是100%违法的,不要被任何借口迷惑。
- 重视自身权益:五险一金是劳动者的基本保障,关系到你的养老、医疗、工伤、生育和购房等重大利益,切勿因短期利益而放弃。
- 入职前核实:在签订劳动合同前,最好通过面试或侧面了解清楚公司是否为员工足额缴纳五险一金。
- 勇敢维权:不要害怕丢掉工作,劳动法是保护劳动者的,而且补缴是公司应尽的义务,维权的成本通常远低于不缴纳五险一金带来的长期损失。
如果情况复杂,建议及时咨询专业的劳动法律师,以获得更精准的法律指导。